初看含平方根和立方根的代数式相比于之前只含有理数的整式计算多了几分复杂。原来一些肯用最直白的硬算死算的方法，在这种含根式题目的计网算里显然无能为力。我们很难精确地表述根式的数值。含无理数的算式里，我们计算变得更难看清结果，事实真会这样吗？其实有理数与无理数之间的恩怨情仇中，是否也充满着我们理解数字的幽默与乐趣。
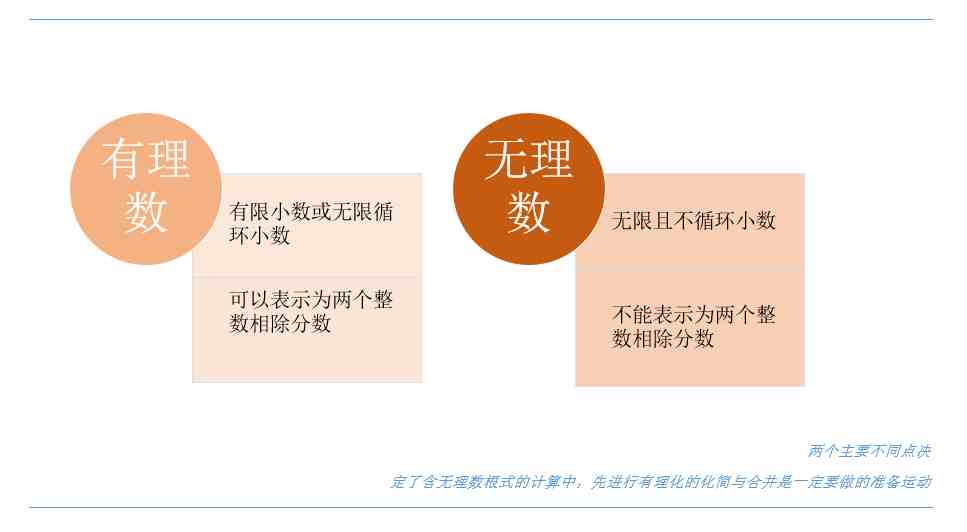
两种数字的不同，正构建根式计算的乐趣
我们初中生学习有理数算式的计算，那么，进行此类计算时，首先，总体方向是将其转化为自己熟悉的类型。计算中的化简一定必不可必，在根式的计算中，应增添有理化的构思；其次，细节上，分析不同方根部分的特点去有理化根式里的具体内容和表述，根据网特点去整理归类、形式有理化的方向；接着，若无法完全有理化的情况下一，进行消除差异或特殊化简，形成消元或降次方，也是有理化的过程；最后，实现用有理数的代数形式解题。具体到原则和步骤如下：
1、原则上，先化简，再求值
2、将无理式进行有理化。建立不同根式中的联系，尽量让根式间内容能互为有理化；
3、分类进行降次或升次的有理化。减少根式项、分母根式有理化。
4、借助数量的几何意义，将根据的关系，用几何图形表示，如用边长网、面积、体积量化。
5、有理化完成后，再进一步合并、消元和降次，实现条件与结果的对接。
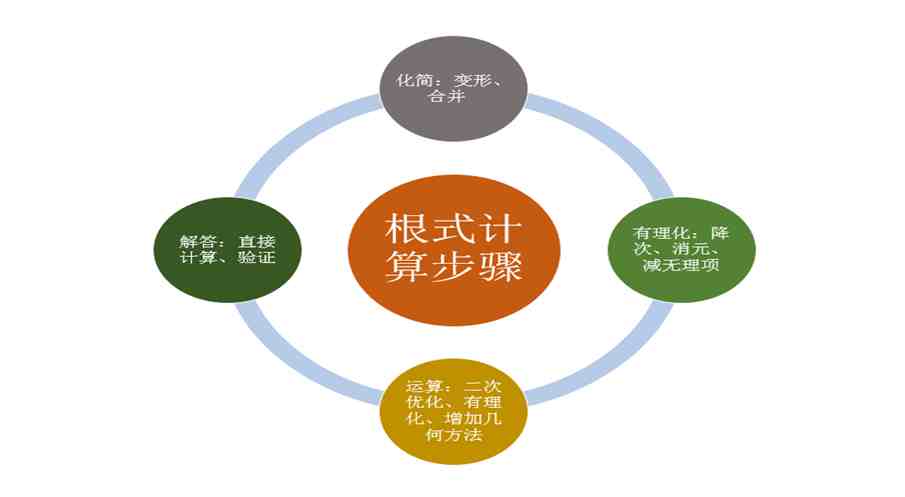
根式计算的简要步骤
例一：化简
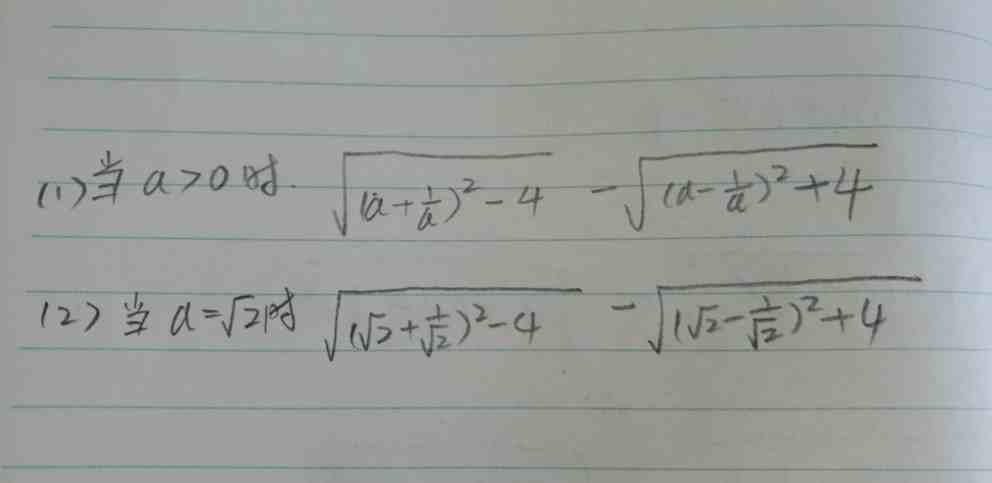
例题一和二的对比
例题一和二，我们都可以发现两种根式内容，从抽象上看是一样，只是前者为字符形式，后者为数字形式，数字形形我们对每个根式进行化简：
解：（1）当我们做第二题时，每个根式直接计算，就可以得到结果为－√2，这时代数计算碰巧还可以解决；
NeWs。KeMaoWANg.oRG。cN（2）直接计算的思路，用于解第一题显然不行，这时只能先进行化简，具体方法如下图
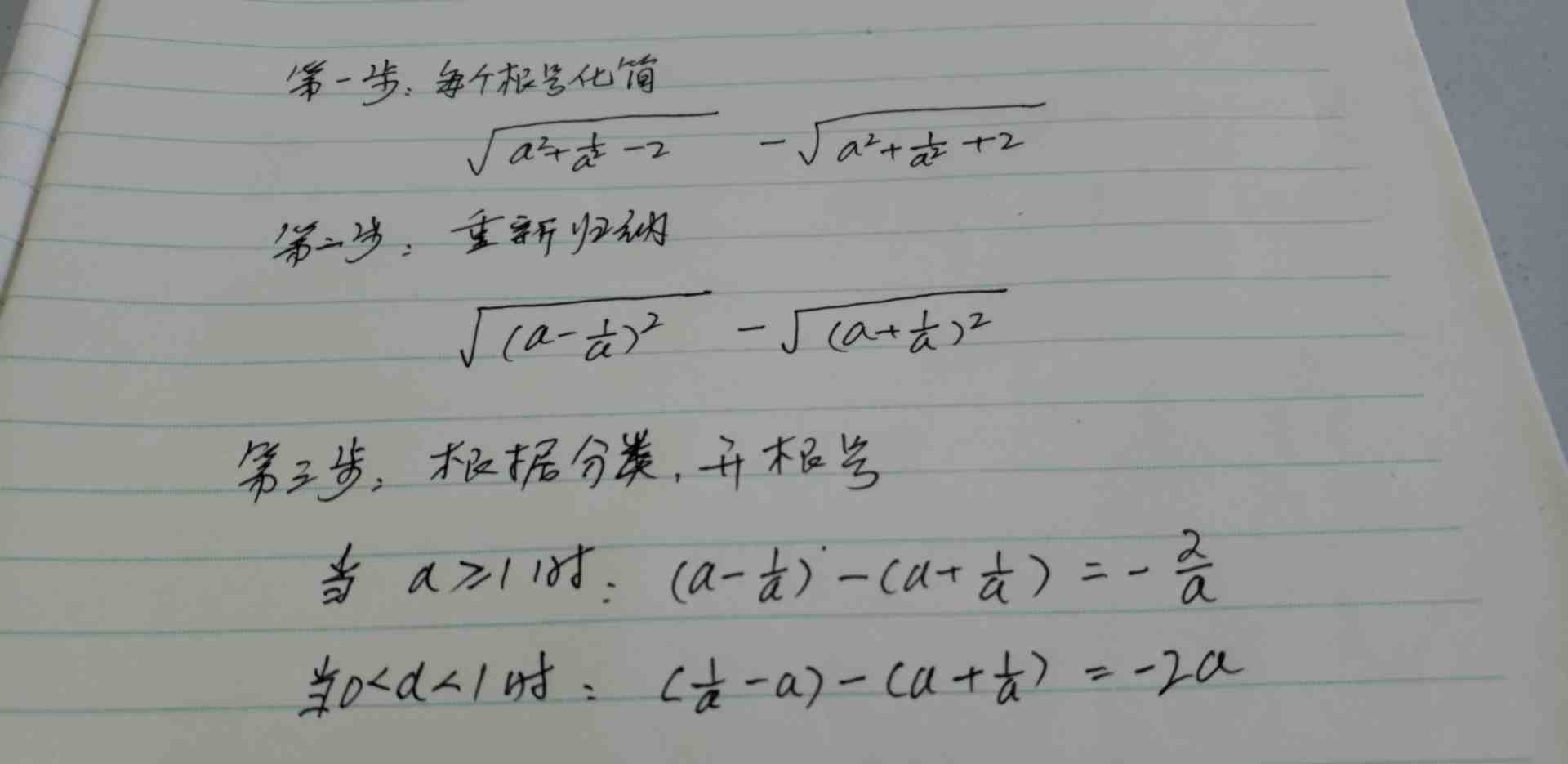NeWs。KeMaoWANg.oRG。cN解题步骤
小结： （1）从上述计算结果看，a＝√2，结果就是－√2，只是一种特例；
NeWs。KeMaoWANg.oRG。cN（2）a
