
neWs.kemaOwanG.oRg。Cn
圆周率日被定为3月14日,为什么?因为的前三位是3.14。得到的值并不容易,有很多种方法可以计算出。这篇文章我将分享一些我最喜欢的方法来获得这个伟大的数字。首先,从一个相当简单的测量方法开始(只是为了与其他方法比较,这样我就可以给出定义)。
是什么?
如果你取一个圆,至少可以测出它的两个参数。一个是绕圆一周的距离(周长),另一个是直径。
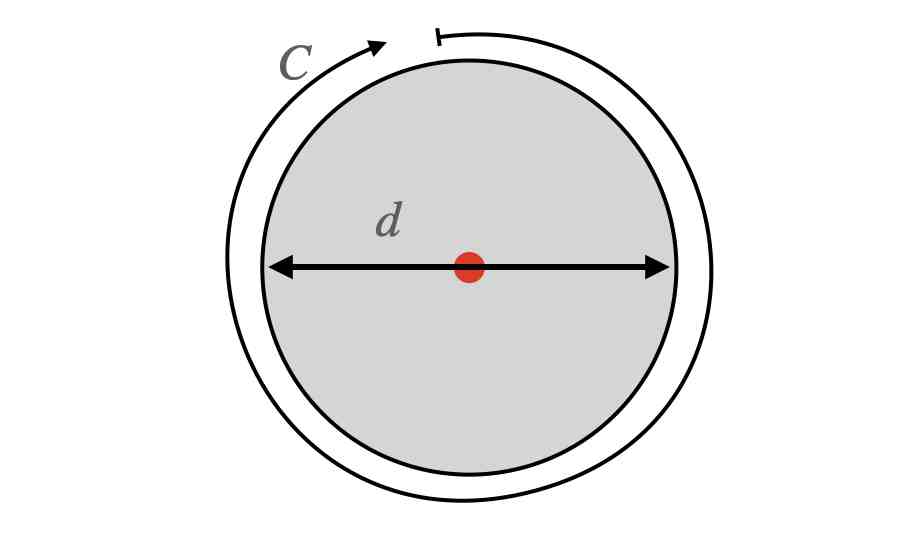
圆的直径越大,周长越大。事实上,这两个变量是成正比的,比例常数就是。
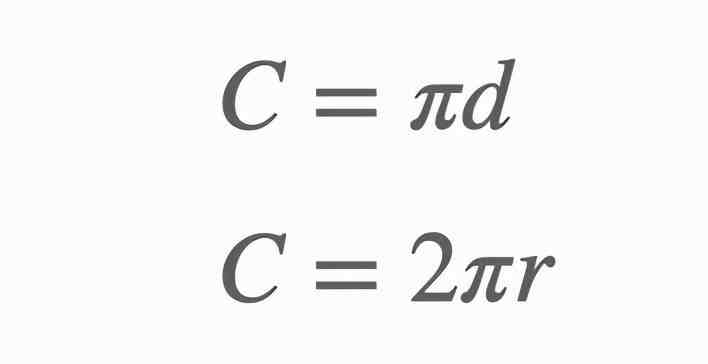
现在我们来看看求圆周率的其它方法。
带随机数的Pi
这叫做的蒙特卡罗计算(Monte Carlo calculation)。“蒙特卡洛”这个词的意思是赌博。这种方法不是赌博,它依赖于随机数。它的原理如下:
假设你取两个随机数,都在0和1之间。现在把这些随机数设为图上的(x,y)坐标。然后你可以用勾股定理计算这个点到原点的距离:
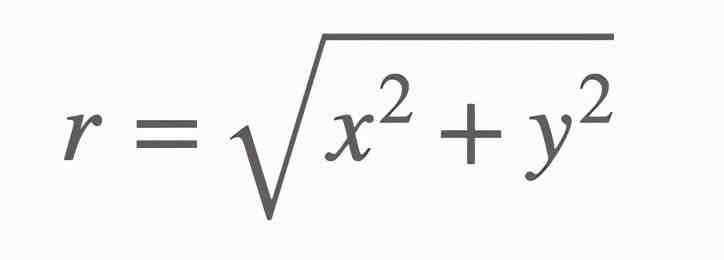
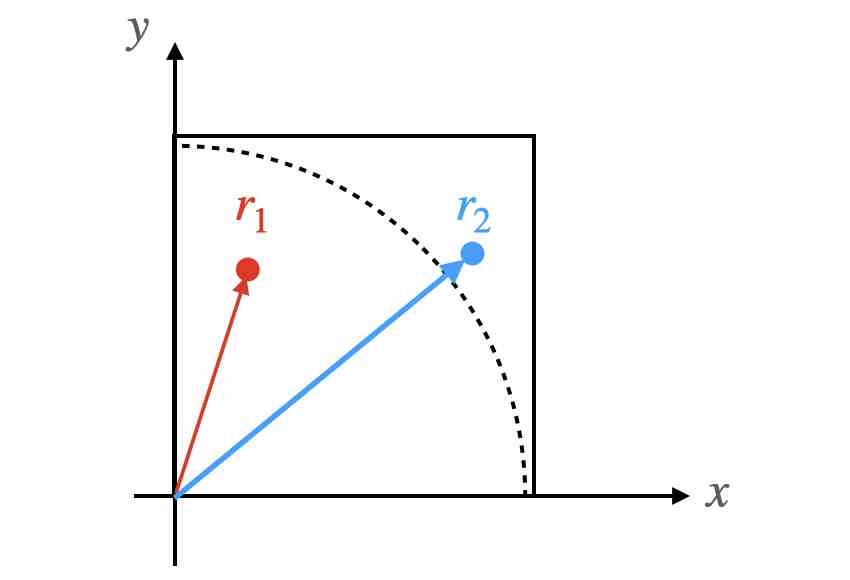
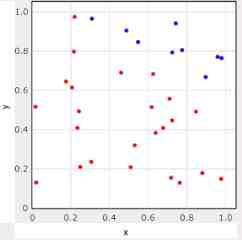
因为x和y都在0和1之间,所以这些点应该都在一个边长为1的正方形内(下图所示)。然而,其中一些点的r值将小于1,而一些点的r值将大于1。
neWs.kemaOwanG.oRg。Cn
蓝色点的r大于1红色点的r小于1。这个正方形的面积是1,红点在半径为1的1 / 4元内。
现在想象正方形内有很多点。如果它们是均匀分布的,那么r小于1的点与总点的比值应该等于1 / 4圆的面积与正方形的面积的比值。圆的面积是r^2。
设r小于1的点的个数设为n,总点数设为N,得到如下关系:
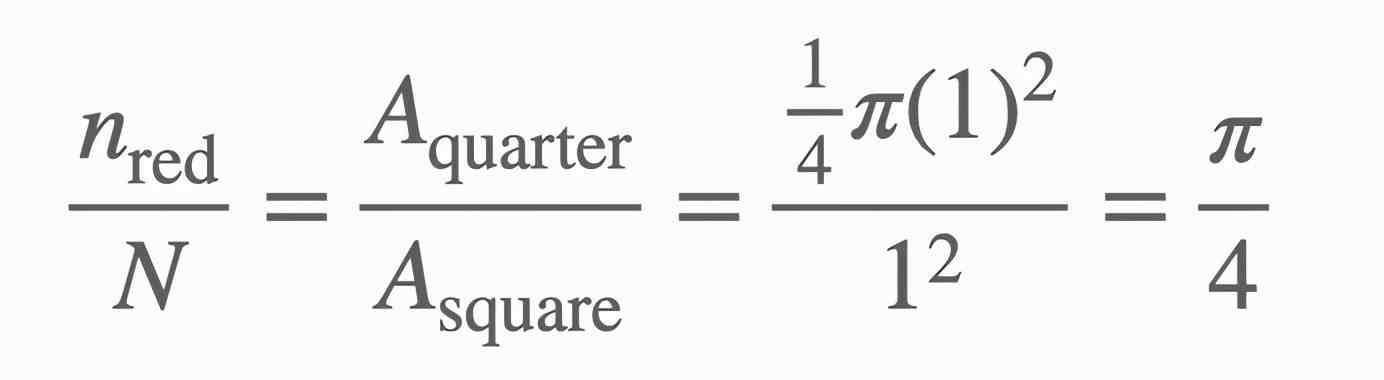
我们只需要随机取一些点并计算它们到原点的距离。我编写一个python程序来实现这一过程。代码很简单:
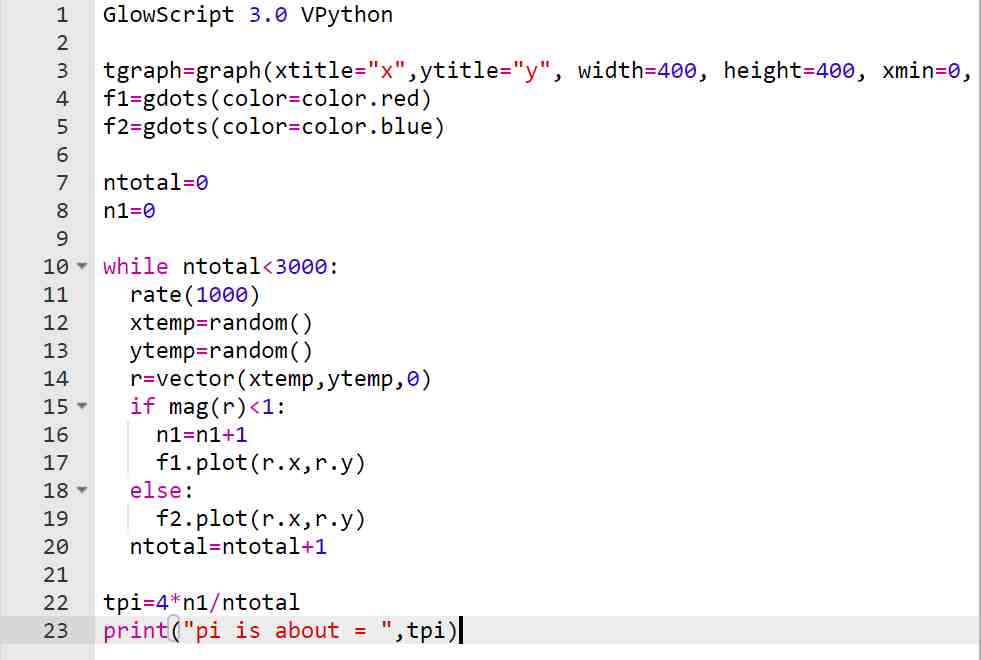
neWs.kemaOwanG.oRg。Cn
虽然这给出了值的估计,但要得到一个较为精确的值可能需要相当长的时间。下面是圆周率作为“点数的函数”的计算值。
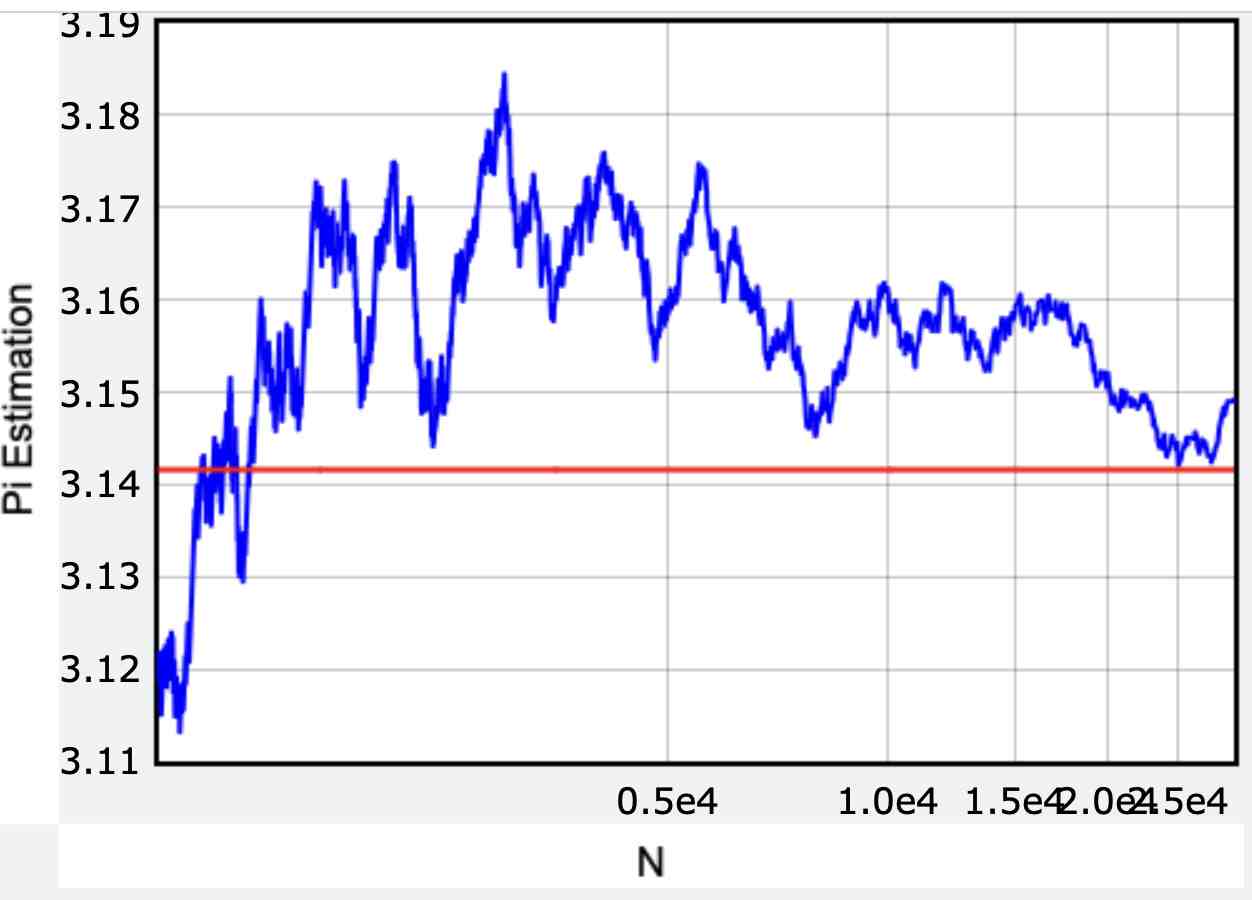
它不是完美的,但也不是太糟糕。
通过砝码和弹簧计算
说实话,几乎每个物理学家都喜欢弹簧。

关于弹簧(理想弹簧),弹簧的力与它的拉伸成正比。我们称之为比例常数,弹簧常数用k表示,因此我们可以用下面的方程来表示弹簧所受的拉/压力。

首先是找到这个弹簧弹性常数k。如果我把不同的物体挂在弹簧上,让它静止,那么弹簧的力就等于物体的重量。网由此得到下图。
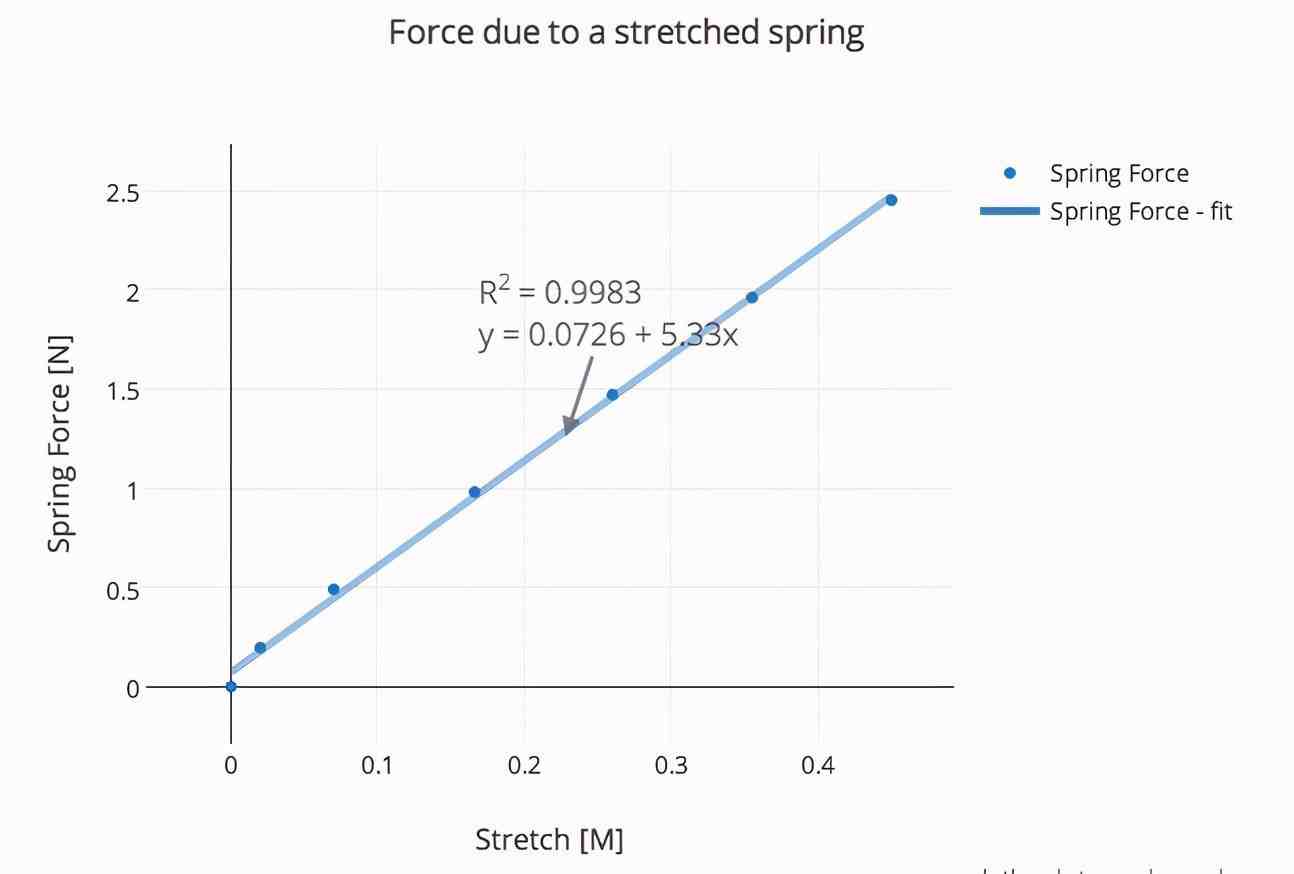
这条线的斜率是弹簧常数。现在,我可以让砝码振荡并测量震荡周期。

如果对这个问题进行数学运算,就能得出,振荡周期(T)同时依赖于弹簧常数(k)和质量(m),关系如下。
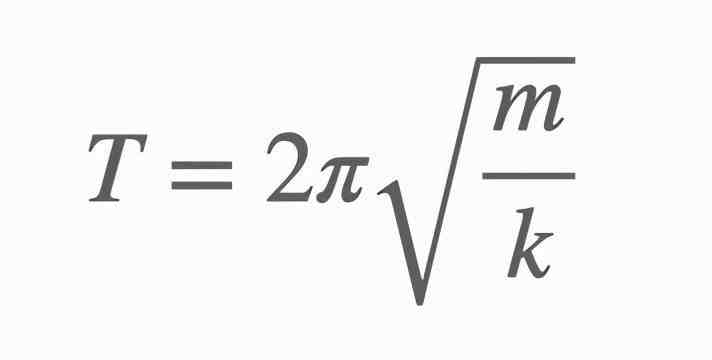
如果我测量周期,质量,和弹簧常数,我可以得到,而这里没有出现圆。
用一个假圆网找到
如果你不想测量一个真实的圆呢?用电脑画一个圆,然后测量周长和半径可能更容易。由此,你可以计算。具体做法如下:
- 在二维中模拟砝码与弹簧的相互作用。
- 弹簧与某个固定的位置相网连,这使得砝码绕一个圆形轨道运动。
neWs.kemaOwanG.oRg。Cn
但是如何找到初始速度使它形成一个圆形轨道而不是其他类型的运动?这里我不计算初始条件,而是让它自己寻找。我只需加一个径向阻力。这是一种力,它只依赖于接近或远离圆心的速度。
下面就是它“寻找”圆形轨道时的样子。

有了一个圆,就可以用到圆心的平均距离来测量圆的半径。周长就是圆周上的步长。
用这个方法,我得到了3.13791,还不错。我认为我最大的问题是找出物体什么时候形成一个完整的圆。
欧拉恒等式
这不是求的方法,但它用一个非常美丽的方程表示了。
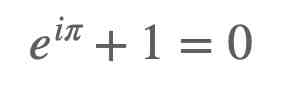
neWs.kemaOwanG.oRg。Cn
这就是欧拉恒等式。它包括了最重要的5个数字。这些数字居然由一个方程式联系起来,这太不可思议了。
想了解更多精彩内容,快来老胡说科学

